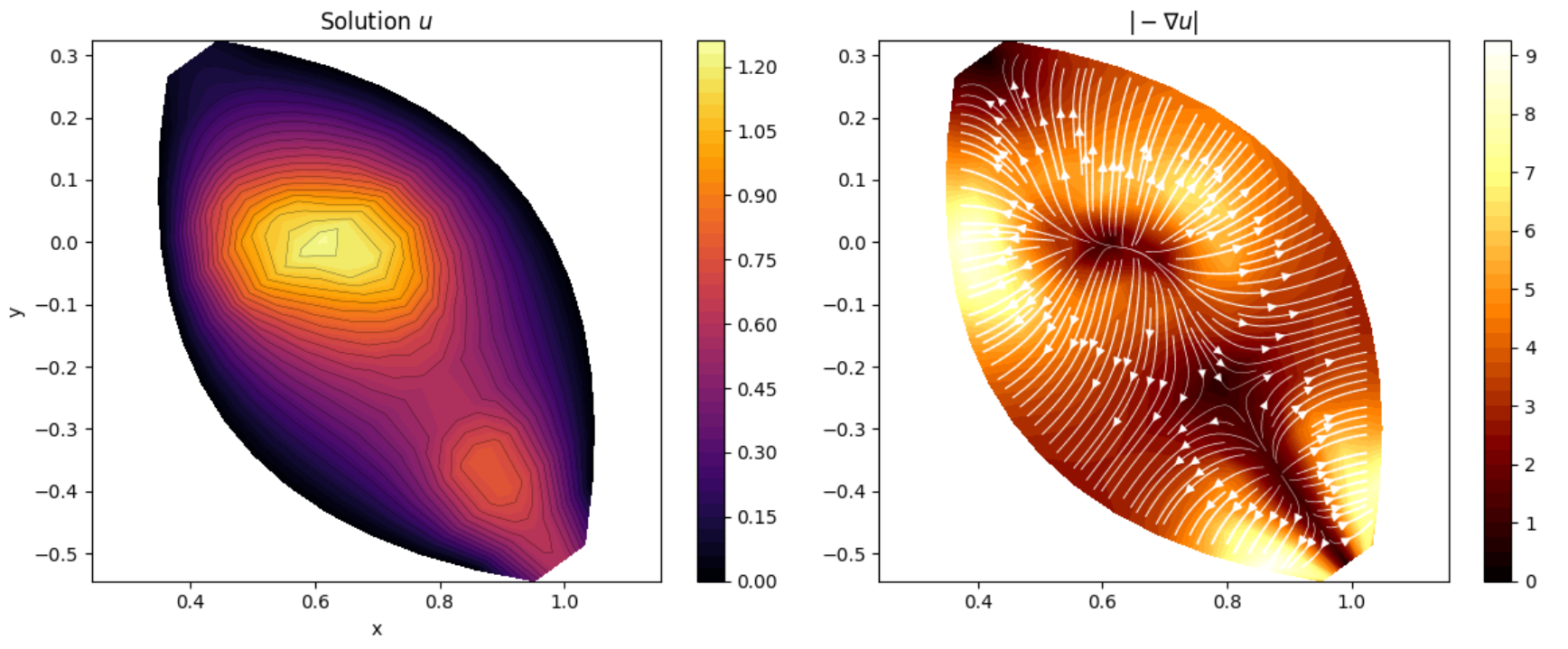
Poisson Equation Solver in Transformed Space
Solving the Poisson equation is a critical task in almost all engineering fields, where it models countless phenomena like gravity and electrical potential. Many different Poisson equation solvers exist, but they rarely support solving the equation in a transformation on curved space. This publicly available project solves that problem by introducing an easy-to-use and lightweight Poisson equation solver implemented in Python that supports curved spaces, available on PyPI and GitHub. The solver supports Neumann, Dirichlet, and mixed boundary conditions, and is designed for ease of use, requiring less than 10 lines of code to set up and execute.
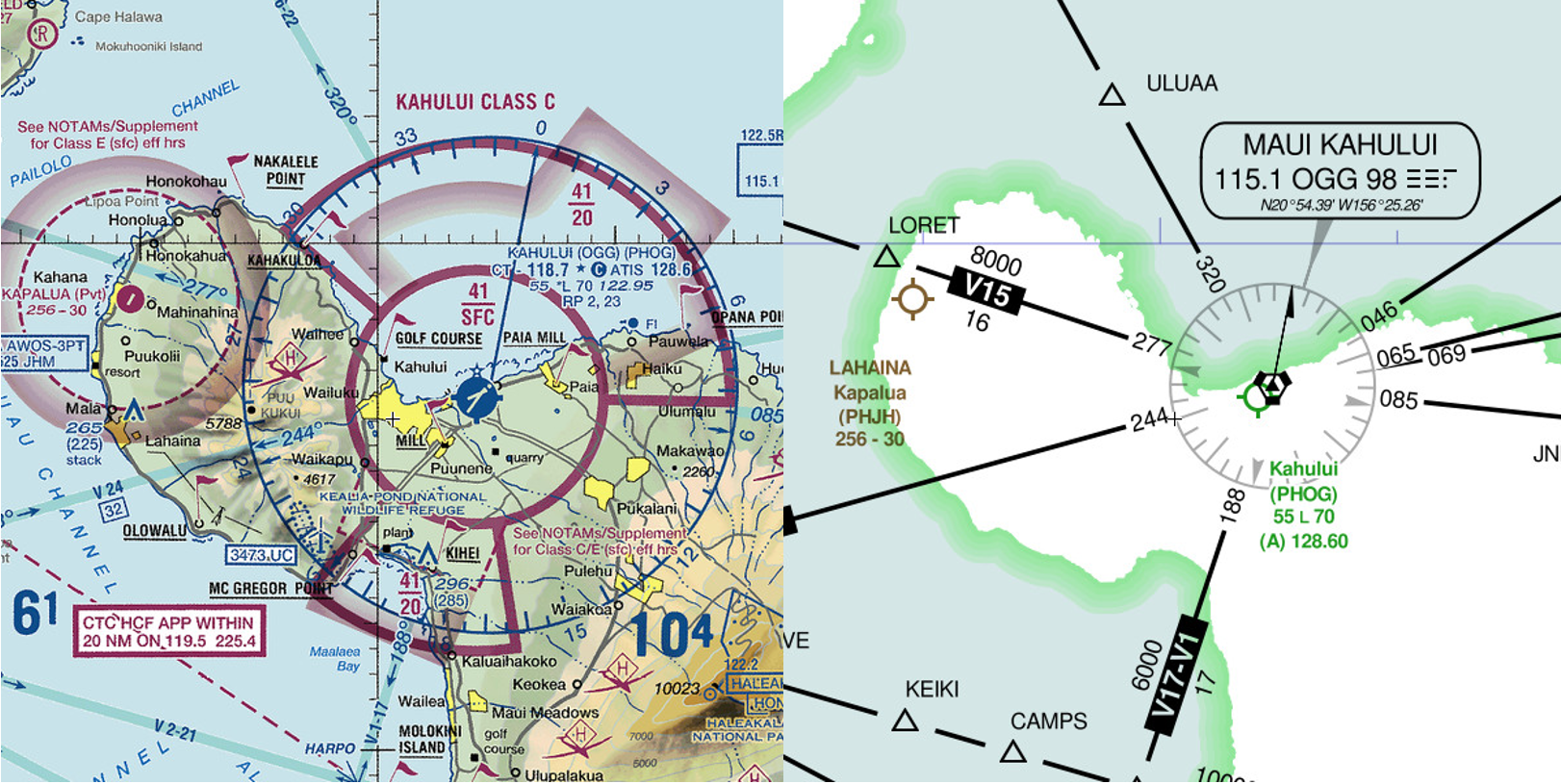
Assessing Spatial Comprehension on Maps in Pre-trained AI Models
Map reasoning is an intuitive skill for humans and a fundamental skill with important applications in many domains. In our blog post, we evaluate the capabilities of contemporary state-of-the-art Large Vision-Language Models (LVLMs) for reasoning on maps and comparing their capabilities with human participants on the coregistration task. We additionally propose and release a novel dataset to serve as an initial benchmark for map reasoning capabilities. We run an extensive analysis on the performance of open-source LVLMs showing that they struggle to achieve good performance on our dataset. Finally, we show that coregistration is intuitive to human participants who were able to reach close to perfect accuracy in a time-constrained manner.
Investigating the Dynamics of the Loss Hessian during training
Recently in ML literature, the Hessian of the Loss in Deep Learning is a topic of great interest. In this work, we derive an efficient analytical computation of both the maximum eigenvalue and the trace of the Hessian of the Loss in addition to an analytical and empirical convergence rate of the algorithm. The algorithm is efficiently implemented using nothing but commonly used Machine Learning techniques: the forward pass and backpropagation. Then, we train over 150 models spanning over 10 thousand epochs with different hyperparameters and optimizers and run the algorithm after each epoch to empirically calculate the properties of the hessian during training. We provide empirical results for the relationship between generalizability and the hessian, in addition to several other observations that arise from this data.

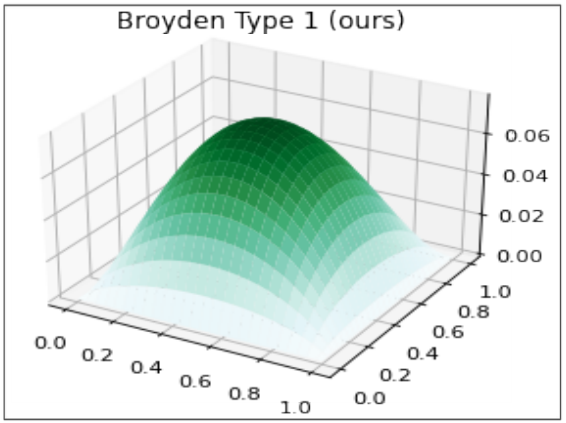
Quasi-Newton methods for nonlinear systems of equations
In this work, we give rise to the motivation of the root-finding problem and the use of Newton’s method within this context. Then, we discuss why one might go beyond those methods to introduce Quisi-Newton methods to which we rigorously derive both types of Broyden Updates along with an efficient implementation of the algorithm. We run my implementation of both types of Broyden Updates along with Newton’s method and an implementation of Broyden Updates provided by the Scipy library on two realistic real-world problems. We finally discuss the application of Broyden Updates in many different areas of science and the different variants of the algorithm that were later proposed.
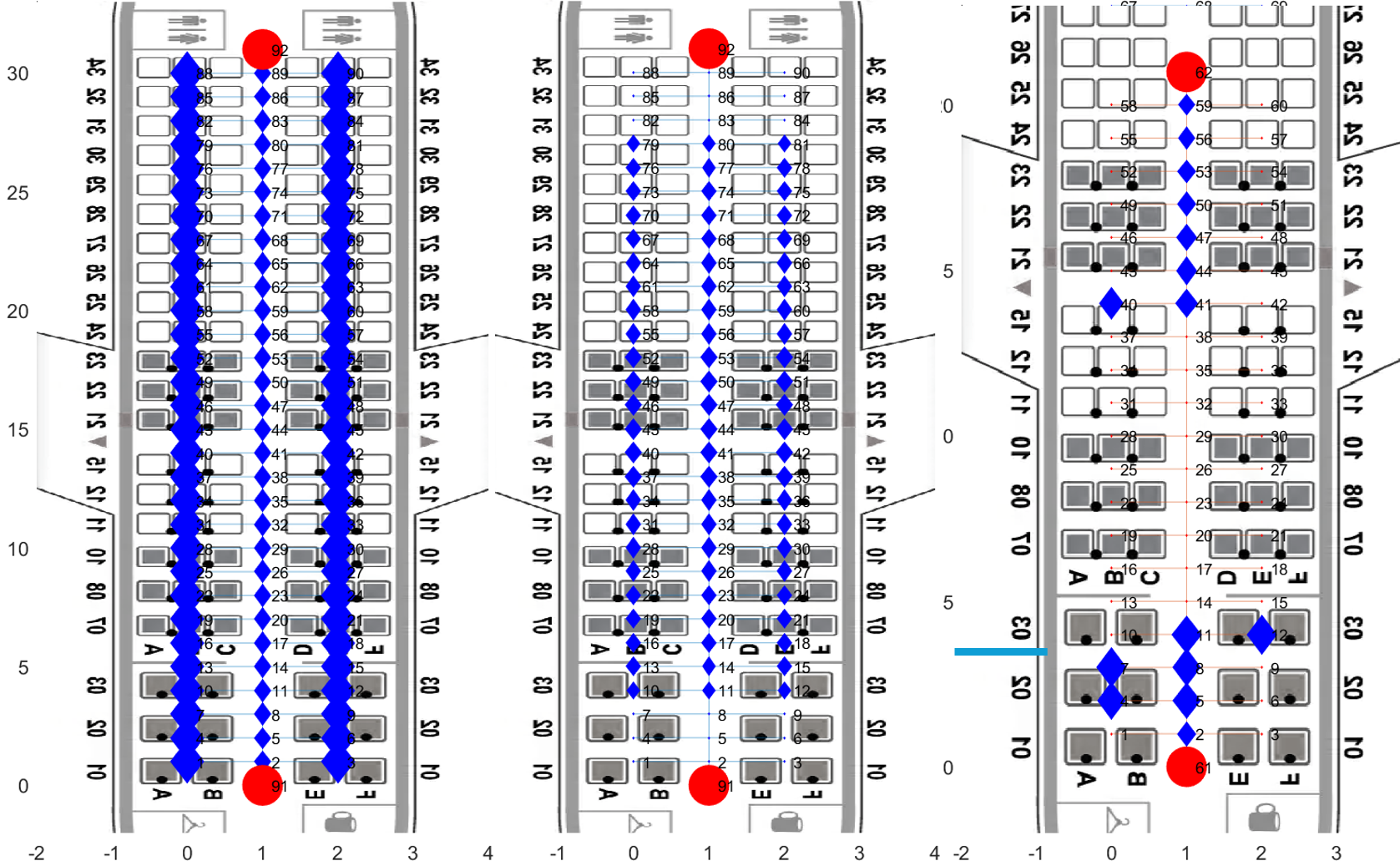
Numerical Modelling of Aircraft Evacuations
The FAA regulation for safe aircraft evacuations requires a demonstration under specific conditions. The current demonstrations are performed without any computational models aiding the design prior to live testing. This project demonstrates how a numerical model can be used to simulate a much wider range of conditions to aid designers in picking a single design to proceed with. Our numerical model is created as an equivalent circuit with non-linear constitutive equations. Employing the model on an example baseline configuration shows the location of bottlenecks and the relative impact of obstacles in the evacuation path. When paired together, a physical demonstration and numerical model can more effectively ensure that an aircraft is capable of a safe evacuation in all conditions, compared to a physical demonstration alone.
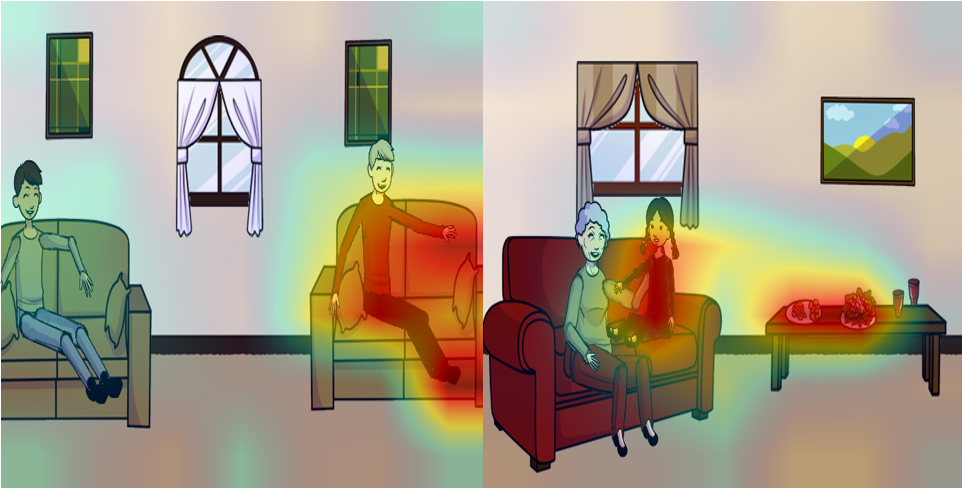
Binary Visual Question Answering using Transformers with raw inputs
In this work, we introduce the Visual-Question-Answering task and the balanced binary visual-question-answering dataset. We propose two models, one that is used as a baseline model which is a latent Joint-Embedding model that utilizes Transformer networks to embed the visual and textual parts of the question. We then propose our main model which is an attention model that also utilizes transformer networks as the backbone and is able to achieve relatively good results and beats our baseline latent Joint-Embedding model with the added benefit of being able to see the attention mask to visualize where the model is looking with respect to the question. Finally, we provide visualizations of our model applied to the test set which shows which parts of the image the model is looking at to answer the question.
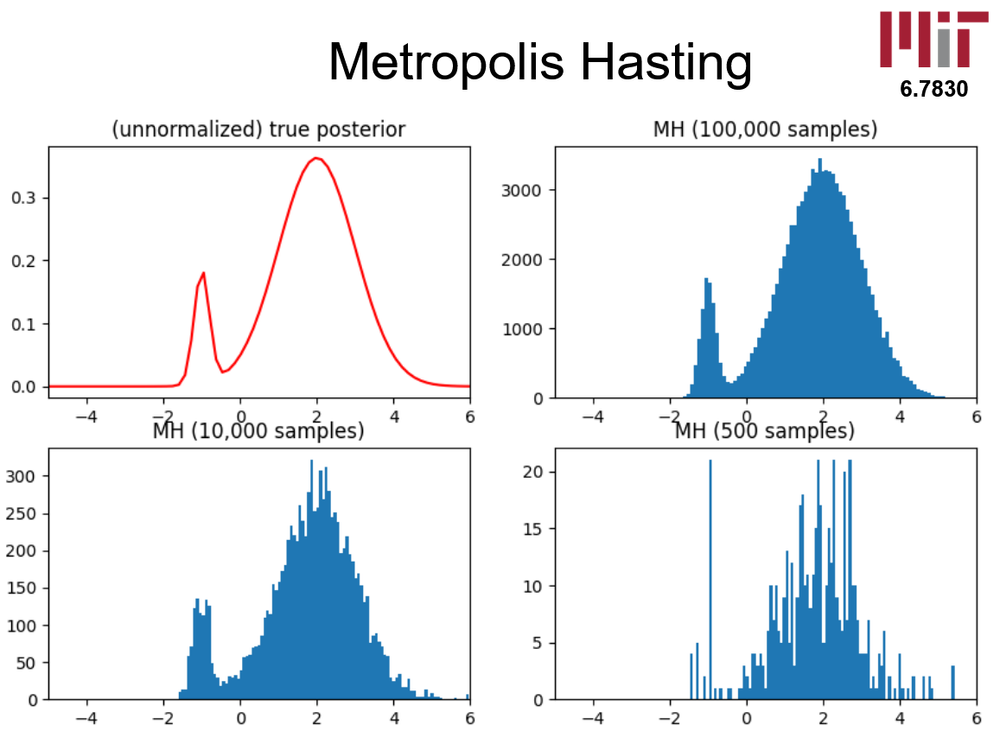
Introduction to Markov Chain Monte Carlo (MCMC)
This is a presentation I made and presented at an MIT class on Bayesian Learning. The presentation introduces the foundational concepts of Markov Chain Monte Carlo (MCMC) to students with prior knowledge of simpler statistical methods, such as rejection sampling and importance sampling. The session explores how MCMC improves parameter estimation in posterior distributions, addressing the limitations of basic techniques. After walking through the theoretical insights of MCMC and some practical demonstrations, the presentation ends with an application of MCMC in a Bayesian learning framework for a model built using Gen. The model detects linear regression parameters for a dataset while simultaneously assigning probabilities for outlier detection.
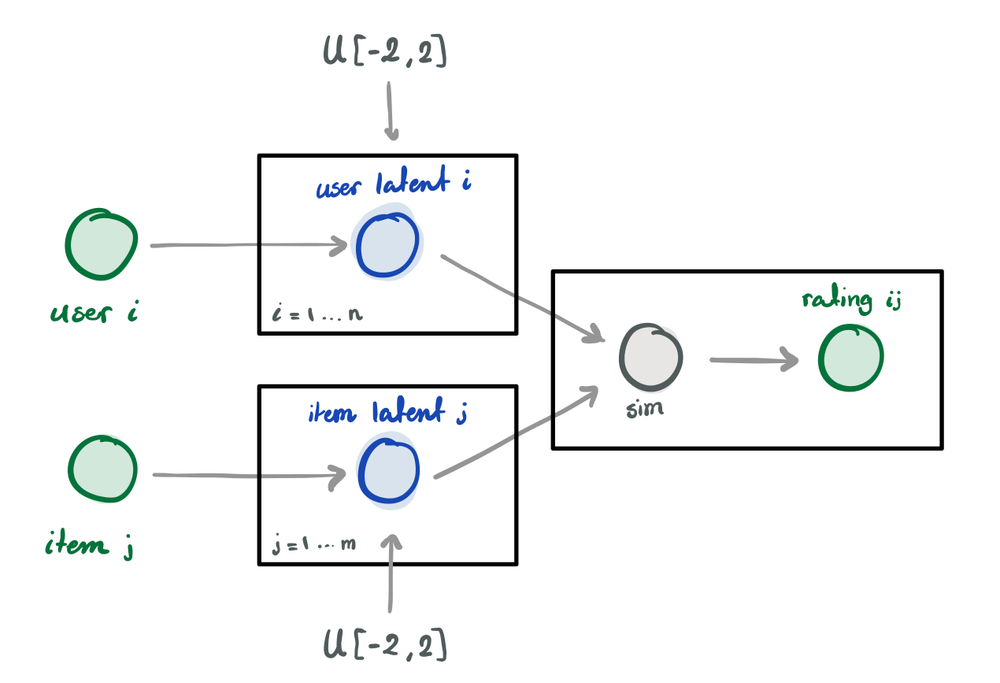
Bayesian Recommender Systems
With the proliferation of data nowadays, recommendation systems have become instrumental in filtering content for the user. These systems curate a set of personalized items to increase user satisfaction. In movie recommendation systems, the algorithm searches for content that would increase the user’s watch time. In this project, we design a Bayesian model to tackle the problem. Our goal is to predict the likelihood of a user liking an item. Experiments showed that our model is able to perform competitively with machine learning models. Moreover, in high confidence predictions, it surpasses them. However, the computational cost and lack of scalability of our model currently pose a limitation to its usage in a large-scale production setting.
Comparative Analysis of Natural Language Methods for Part-of-Speech Tagging
This project is a comparative analysis between large language models (LLMs) and traditional methods for part of speech tagging of natural language using a tagged subset of the widely used Penn Treebank dataset and a domain-specific dataset from the BioNLP STc challenge. LLMs, such as GPT-3 and BERT-style models, have shown remarkable performance in various NLP tasks, including part of speech tagging, and may offer advantages in terms of their ability to capture contextual information and handle long-range dependencies compared to more traditional methods. On the other hand, more traditional models have been widely used for part of speech tagging, exemplified by parsers such as the Stanford Parser, and the part of speech taggers available in the Natural Language Toolkit (NLTK) library in Python. We evaluate the accuracy of several models and provide insights into the strengths and weaknesses of each approach for part of speech tagging. This information informs the choice of modeling technique for similar applications and contributes to the understanding of the trade-offs between LLMs and PCFGs in part of speech tagging of natural language text.
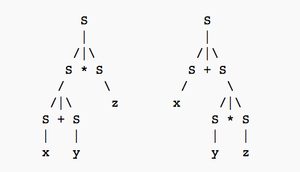
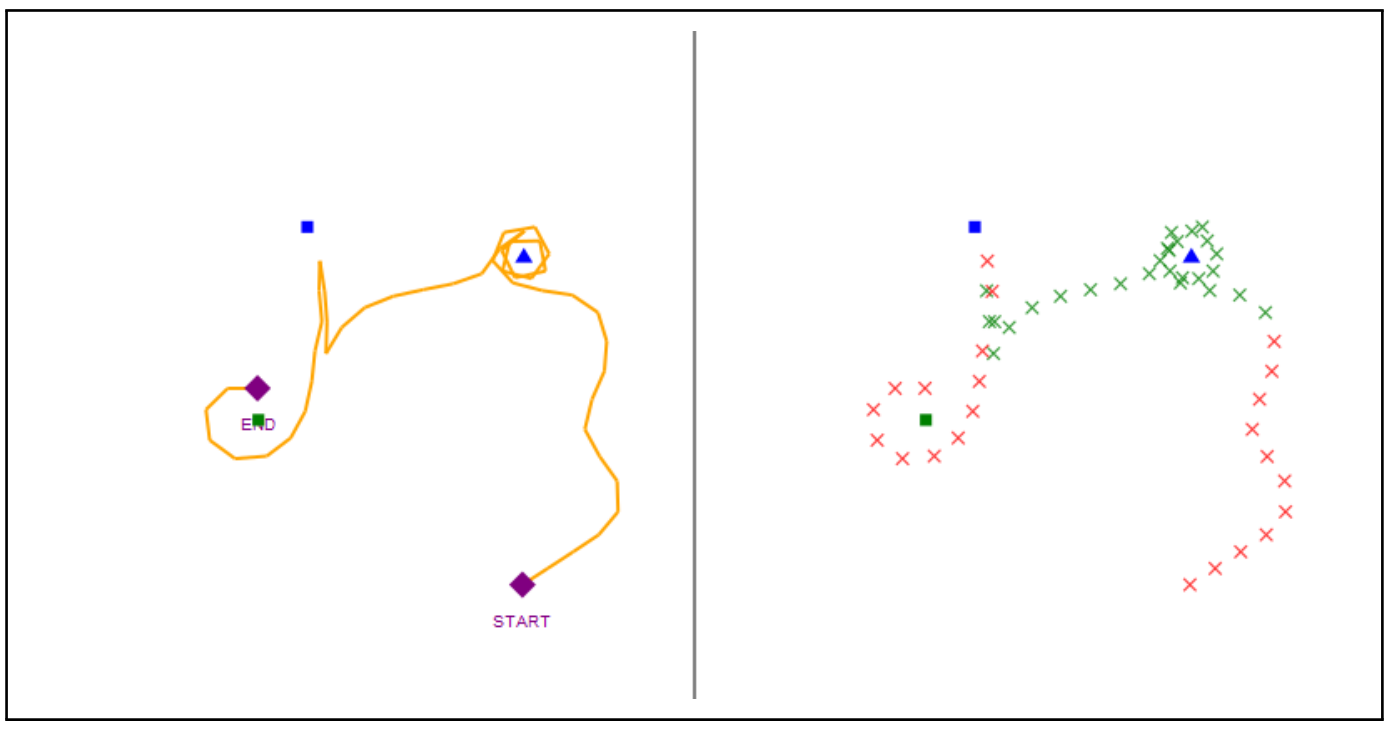
Identifying Symbolic Communication in a Simulated Teacher-Student Environment
Symbolic communication is an inherent and intuitive aspect of the human experience. In this project, we propose, implement, and run inference on a probabilistic Bayesian model for identifying symbolic communication. We focused on a recently proposed simulated teacher-student environment where we have access to human data. We show several qualitative and quantitative results that compare our model with human judgments. These results suggest that our approach is reasonably effective at identifying symbolic communication with adequate accuracy. We utilize the Gen probabilistic programming framework for the implementation of our model.
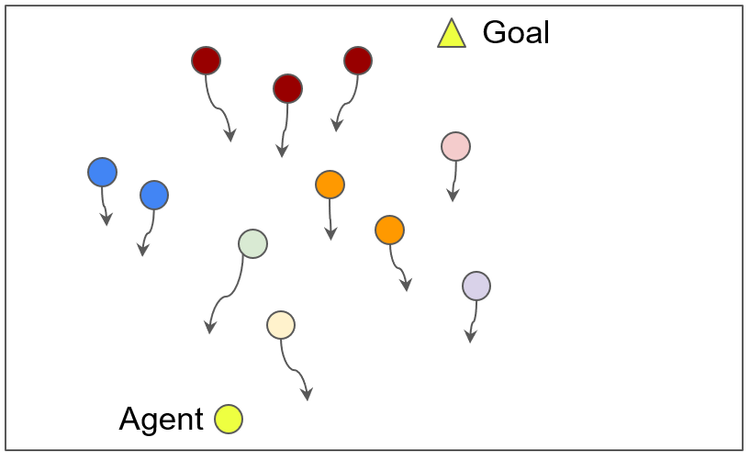
Learning to Navigate in Human Crowds
Social robot navigation requires that the robot follows social norms while navigating towards its goal. Current algorithms model pedestrians as independent agents, making the problem computationally intractable and degrading overall performance in dense human crowds. In this work, we explore various ways to enhance the robot’s performance in environments with a higher number of pedestrians and aim to achieve well-behaved scaling. Specifically, we compare different approaches common in the literature such as state reduction, reward shaping, and curriculum learning. We find that the use of curriculum learning closely approximates optimal (human-like) behavior. The report serves as supplemental information, while the presentation includes the results of the experiments including animated visualizations.
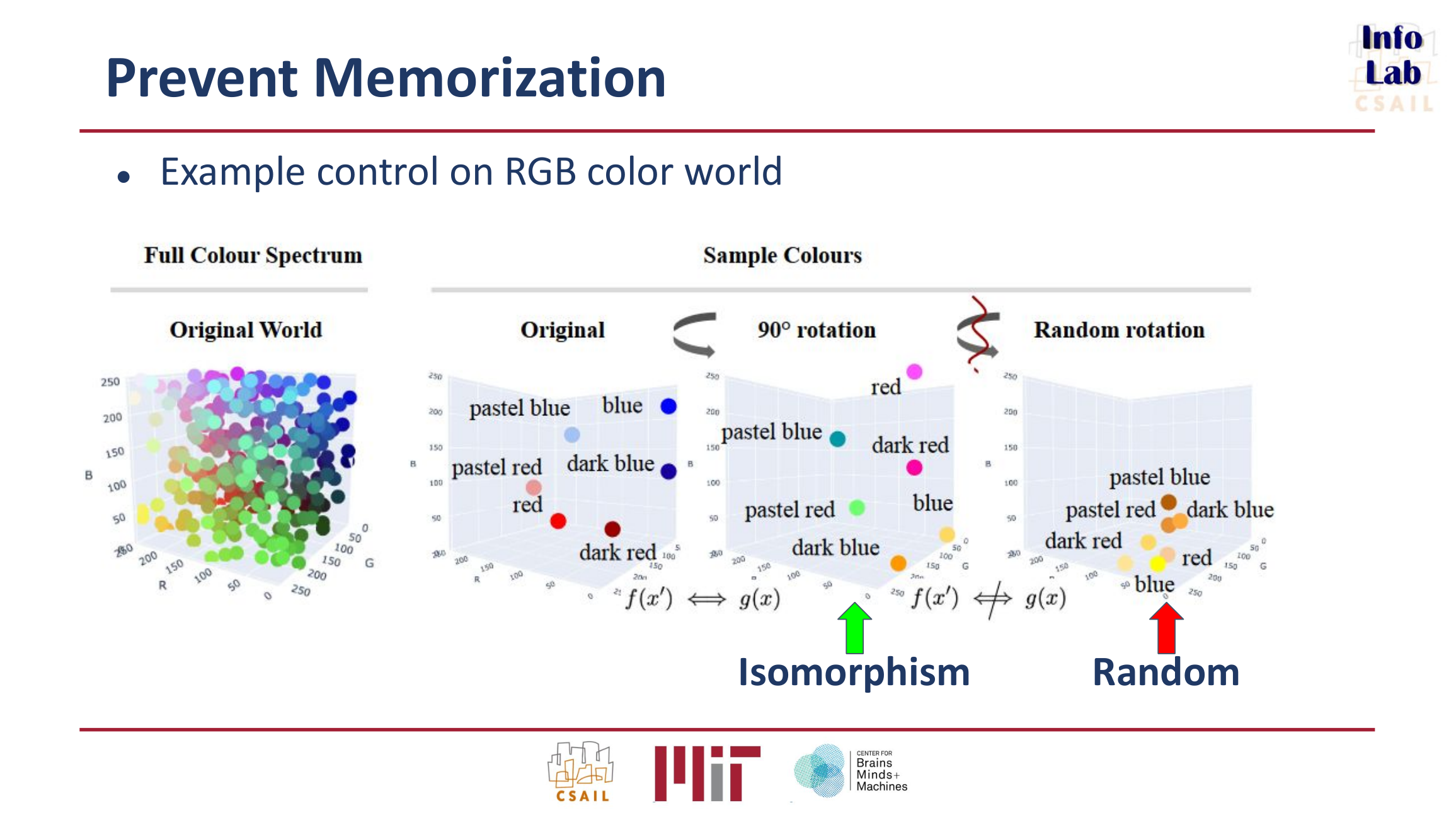
Paper Recap: Mapping Language Models To Grounded Conceptual Spaces
This is a presentation I made and presented at an MIT class on large language models by Professor Yoon Kim. The presentation is a recap of the paper "Mapping Language Models to Grounded Conceptual Spaces" which addresses a critical limitation of text-only language models: their lack of grounding, or the ability to connect linguistic representations with real-world referents. Despite this challenge, the paper demonstrates that these models exhibit a robust conceptual understanding, enabling inference and fluent text generation. Our presentation summarizes the key findings of the paper and then introduces original experiments that explore this alignment further. Our results reveal both supporting evidence that confirms the paper’s findings and contrasting outcomes that highlight areas of disagreement.